High-dimensional complex data presents complex structures such as multiple subspaces and nonlinear manifolds, making it difficult to characterize the statistical properties of the data. Furthermore, it often contains strong noise, missing values, and other interfering information, leading to errors or even the inability to execute downstream tasks. Developing mathematical tools that can both describe the intrinsic structure of the data and eliminate interference is one of the core challenges in the field of data analysis and a fundamental problem in artificial intelligence and related fields.
In response to these challenges, Zhouchen Lin’s team noticed that low-dimensional subspaces and low-dimensional manifolds correspond to low-rank data matrices. Therefore, they used rank constraints to help separate the low-dimensional main structures of the data from scattered noise structures. Based on rank as a fundamental mathematical tool and combining techniques such as spectral graph theory and Lagrange multiplier method, they proposed low-rank models, theories, and efficient optimization algorithms that can robustly extract multiple subspaces and manifold structures. This work has made creative contributions to the theory and algorithms for analyzing high-dimensional complex data.
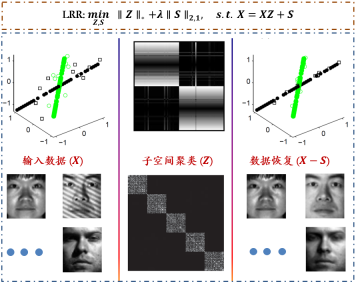
The main findings are as follows:
1.For the robust subspace clustering problem with strong noise, the rank was found to be an effective tool for characterizing the structures of multiple subspaces. This led to the proposal of the Low-Rank Representation (LRR) model, which simultaneously addresses the extraction of subspace structures and data denoising. Further theoretical analyses were provided for LRR, including strengthening the conditions for the block diagonal structure of the coefficient matrix and regularization terms, as well as conditions for accurate recovery of the underlying multiple subspaces. These findings have led the research direction of subspace clustering based on low rank.
2.For more complex real-world data, a key extension of the first finding was made, greatly expanding the application of the low-rank model. The latent low-rank representation model was proposed to solve the subspace clustering problem with insufficient data. The non-negative sparse Laplacian low-rank representation model was introduced to overcome the limitations of LRR for nonlinear manifold data. New tensor rank and tensor nuclear norm were defined, and a complete theory of data completion, denoising, and subspace clustering for tensor data was reconstructed. The robust principal component analysis theory proposed by E. Candès, a member of the National Academy of Sciences and inventor of compressed sensing, became a special case within this framework.
3.To address the computational complexity of solving low-rank models, several Lagrange multiplier algorithms were proposed by utilizing the structure of low-rank models, combining techniques such as adaptive penalty parameters, linearization, and parallel splitting. An iterative reweighted nuclear norm contraction algorithm was also developed, which achieved convergence speed improvements ranging from 3 to 1000 times for different problems.
Representative papers of Prof. Lin’s team have been cited nearly ten thousand times on Google Scholar and have received positive evaluations from over 100 academicians and fellows of mainstream societies such as the ACM and IEEE, both domestically and internationally. The proposed models and algorithms have been applied to modeling and solving over 100 practical problems, resulting in significant international impact. The achievements were awarded the First Prize in Natural Science of the 2020 China Computer Federation (CCF) Science and Technology Award, with Lin Zhouchen as the first author.



